AoC 2024

** Day 1: Historian Hysteria – Two columns of integers; compute their "distance" and "similarity"

Part 1

int()

abs()

sum()

Part 2

zip(*data)

collections.Counter()

** Day 2: Red-Nosed Reports – List of reports containing levels that, to be "safe", must be all increasing or all decreasing

Part 1

itertools.pairwise(data)

all()

Part 2

any()

data[:i]+data[i+1:] OR [data[di] for di in range(len(data)) if di!=omit_i] OR itertools.compress() OR ...

** Day 3: Mull It Over – "mul" commands mixed into corrupted memory contents

Part 1

This is very much a problem for using the re module.

sum()

Specifically...

re.findall OR re.finditer OR re.match

Part 2

Yet more re...

Specifically...

re.finditer OR re.split

** Day 4: Ceres Search – XMAS word search

Part 1

Probably use the zip trick mentioned in the overall AoC commentary:

def func(... rc ...):
  ...
  for drdc in [ ... ]:
    r, c = rc
    for i in range(...):
      ...
      r, c = [sum(z) for z in zip([r, c], drdc)]

Additionally...

Instead of loading the data into a list of lists, you may wish to load it into a (row,col)-tuple-keyed dictionary containing actual grid-content as those keys' corresponding values. For example, if reading in grid-arranged characters:

with open("input.txt") as infile:
  grid_dict = {(r, c):char for r, line in enumerate(infile) for c, char in enumerate(line.rstrip('\n'))}
  # as compared to: grid = [list(line.rstrip('\n')) for line in infile]

This makes it more straightforward to check for out-of-bounds situations, e.g., compare these:

if 0 <= r < len(grid) and 0 <= c < len(grid[r]): ...
if (r, c) in grid_dict: ...

Using a dictionary also may provide an opportunity to entirely avoid explicitly checking this by leveraging use of the dict.get function:

grid_dict.get((r, c), def_val) ⟶ if (r, c) is in grid_dict, its value is returned; else the provided default value is returned

Part 2

words = set([word, word[::-1]])

** Day 5: Print Queue – Page-pair-order rules, lists of updates, and establishing their validity

Part 1

sets/frozensets and dictionaries may be helpful for solving this problem a bit more efficiently. (But, it's not a computationally intensive enough problem to make their use critical.)

Part 2

functools.cmp_to_key

** Day 6: Guard Gallivant – Guard patrolling a grid, with obstacles

Part 1

I used a direction vector as the heading, i.e., a 2-tuple expressing the (row,col) direction the guard is moving (e.g., (-1,0) as the initial (dr,dc)), then changed it mathematically for each turn via a simple matrix multiplication:

𝐇_{n e w} = [\begin{matrix} 0 & 1 \\ - 1 & 0 \end{matrix}] [\begin{matrix} 𝐇_{o l d} [0] \\ 𝐇_{o l d} [1] \end{matrix}] = (𝐇_{o l d} [1], - 𝐇_{o l d} [0])

This approach works nicely when there are a variety of possible actions upon encountering an obstacle. However, in this case there's only one action ever taken at an obstacle ("turn right"), so there are arguably "simpler" (more easily understood, anyway?) ways of dealing with this, such as iterating through a list of headings repeatedly (or something similar), e.g.:

hdgs = [(-1,0), (0,1), (1,0), (0,-1)] # headings: up, right, down, left
hi = 0 # initial heading (index)
hi = (hi+1)%4 # turn right (every time, regardless of what the current heading is)
pos = [sum(z) for z in zip(pos, hdgs[hi])] # move position one step in direction of current heading (i.e., hdgs[hi])

Something similar, and functionally equivalent (but probably slightly less efficient due to moving data around):

hdgs = [(-1,0), (0,1), (1,0), (0,-1)] # initial headings: up, right, down, left
hdgs = [*hdgs[1:], hdg[0]] # turn right (every time, regardless of what current heading is)
pos = [sum(z) for z in zip(pos, hdgs[0])] # move position one step in direction of current heading (i.e., hdgs[0])

Part 2

Adapt Part 1's solution into a repeatable "is_looped" function that returns whether or not the guard's path is looped, and which can be run for every possible obstacle-placement that needs to have this tested.

How do you determine "is looped" or not, though?

"Is not looped" should be easy to determine: it's the same exit condition as in Part 1.

"Is looped", though, might be slightly tougher to detect. I built a dictionary as I went, which recorded 2-tuples of visited locations as its keys with corresponding values being sets containing headings when visiting those locations in the past. If the guard ever revisits the same location while heading in the same direction as at some point in the past, the path is looped. (I suppose this could have just been a set containing (pos, hdg) tuples of tuples.)

Which points do you need to check for obstacle-placement causing loops?

It will work just fine to check placing a single obstacle at, respectively, every single point on the grid that isn't already an obstacle (or the guard's starting position).

But, we can do better...

A simple improvement is to compute the original guard path (from Part 1), and then only place obstacles on that path's positions. Anywhere off that path is irrelevant, not affecting the guard's path at all.

** Day 7: Bridge Repair – Target value, list of numbers, and left-to-right evaluated operator combos

Part 1

You can, of course, parse the input using str.split calls, but you can also directly pull all integer strings out of each line using re.findall(r"-?\d+", line). (Or, use re.finditer.)

This can be implemented most straightforwardly using the itertools.product function.

(It could also be done either recursively or with an iteratively driven "work queue" (see the collections.deque type) so that at each stage, all possibilities are explored.)

Part 2

This probably doesn't require much change to your code. The very simple approach is int(str(a)+str(b)), though that may not be as efficient as other possible approaches. (However, it should be more than "efficient enough".)

One possibly more efficient alternative is int(f"{a}{b}") since f-strings are rumored to be highly optimized.

** Day 8: Resonant Collinearity – Antennas and their antinodes

Part 1

Using zip for dealing with "vectors" is probably a good idea for this one (both for computing differences and sums).

Also, look up itertools.combinations.

Part 2

Just loop some pieces of Part 1.

** Day 9: Disk Fragmenter – Disk defrag

Part 1

(Friend) Check out the grouper recipe in itertools; it might be helpful in converting the input into the starting disk layout.

If representing the disk as a list, pop() from the back and then index() to find the left-most open space.

Note: Representing all disk blocks in a list seems non-optimal, and it shows in the run-time. There's probably a better solution to this one.

(Me) For this one, I made a list of the fully expanded disk contents where files' indices contained their respective IDs, and gap (free space) indices contained Nones. Then, I simultaneously iterated from the start rightward and from the end leftward (until the iterators collided, at which point I was done). The start iterator iterated past files to gaps, and the end iterator iterated past gaps to files and incrementally copied them into the start-iterator's locations. I didn't bother popping/deleting/inserting anything, but simply set the value at the proper location and continued onward. At the end, the list is effectively as long as where the iterators collided, even if it's actually longer than that... just compute and sum the checksums only up to that point within it. The code very quickly completed execution.

Part 2

(Friend) Like Part 1, the strategy here can almost certainly be improved on. Start with the same disk representation as Part 1, and add a dictionary to be an index of where all the blocks are (key is the block identifier, value is a tuple containing block size and block position). Also create a list of gap information (each element is a list containing a gap size and gap position; use a list instead of a tuple because gap entries need to be mutable).

When moving blocks, iterate down from the largest identifier to move right-to-left. For each block, iterate through the gap list to find the first gap that is big enough to fit the block. Be sure that the block is actually moving left – once you've moved enough blocks, some of the "gaps" will actually be totally free space to the right of the current block.

Again, this is a pretty ugly solution. There's probably a way to do this without representing every block individually that could be done much more efficiently.

(Me) I thought of some good ideas and re-wrote my solution.

Without commenting on my original solution's approach (which had elements of similarity to the above), I'll just say that I wasn't satisfied with it since it was relatively slow, despite being effective. This improved reimplementation resulted in both less code and a 10x+ speed-up.

The fundamental insights incorporated were these:

Build two dictionaries, one for the files, and one for the gaps (free space). Key each entry to its location on the disk.
- Files are keyed by their left-end locations (and extend rightward).
- Gaps are keyed by their right-end locations (and extend leftward).
- Corresponding values are their respective sizes on disk (and also file id, for files).
Build a list of the reversed keys from the file dictionary, so that the dictionary can have entries deleted/created while iterating through the list.
- Each loop, a specific file is either moved, or it's not. (Determined by iterating through the gap dictionary for as long as needed.)
  - If it is, then you create a new location-key entry in the file dictionary for the same value, and delete the old one; if not, then just move on.
  - Either way, you're done forever with looking at that file, so you don't care about updating any keys in the reversed key list.
- And, of course, if you moved the file, then you also update the destination gap's size. (If its size drops to zero, delete the entry from the gap dictionary.)
- Iterate (the outer loop) only for as long as the first gap key is less than the current file key.
Finally, you can direct-compute the files' checksums (thereby reaching the final answer), regardless of the file dictionary's key-order. There's no need to expand or sort anything.
- For each entry, you have the id ( $i$ ), location ( $ℓ$ ), and size ( $s$ ), which means you can use the closed form sum of all the numbers from 1 to $n$ to your advantage: $n (n + 1) / 2$ . That is, compute this sum for the end location of each file, and subtract the same computation for one-less-than-the-start location.
- So, each checksum is: $i ((ℓ + s - 1) (ℓ + s) / 2 - (ℓ - 1) (ℓ) / 2)$
  $= i (s (s + 2 ℓ - 1) / 2)$
- Sum them all for the answer.
I put itertools.accumulate to good use at the start.

This approach is much, much faster because there's no "data expansion", no real data movement, and the checksum computations aren't iterative (based on file size).

Side note...

...this problem may be a reasonable place to use linked lists.

** Day 10: Hoof It – Scoring/rating hiking trails

Part 1

For each trailhead, I used Breadth First Search (BFS) to incrementally expand outward until there was nowhere else to go, adding to a set any peak locations I encountered along the way and returning that set's length at the end.

However, in retrospect, Depth First Search (DFS) is the better choice here. One approach is to—for each trailhead—keep track of visited locations and do not move to any position that has already been visited. This way you don't count any peak more than once, and you don't re-explore previously explored paths.

Part 2

Adapted from Part 1, still using BFS to expand outward from the given trailhead, I built a graph to any/all peaks it eventually reached, then I pruned back any trails that didn't reach any peak. Then, I traversed that graph, counting every trail from the trailhead to all the peaks it reached. (I did slap on a @cache decorator, though it didn't end up being necessary for the given input data.)

But, if you used a DFS strategy in Part 1 (like a friend did), there's almost nothing to do for Part 2. You no longer need to track visited locations, because now you want to know all the different ways to arrive at each peak. That's the only significant change, and it's a code simplification/reduction!

** Day 11: Plutonian Pebbles – Stones that change when you blink

Part 1

This problem is fairly easy (and computationally feasible) to solve via the obvious/naïve approach.

Part 2

This problem is not as computationally unconstrained as Part 1 is.

I suggest using...

...dynamic programming.

Use the fact that...

...every stone may be independently processed from every other stone.

Recursive parameters can be...

...just the number of the stone being processed, and the number of blinks remaining to hit the initial target blink count that starts the process.

** Day 12: Garden Groups – Computing the costs of fencing garden plot regions

Part 1

Write a function that can extract a full region (garden plot).

I'd suggest...

...using the zip of location and delta approach, and recurse to all the neighbors while tracking where you've been. The use of sets is a good idea.

It should then be trivial to determine the region's area. So, write a function to determine its perimeter, and compute the final answer using the two.

You could...

...iterate through the region's members (extracted by the preceding function) and increment a running total every time you find a "neighbor" that's not in the region.

Note that the grid's letters...

...don't really matter at all, other than just for specifying a blob representing a region's shape/connectivity. Once a region is extracted, the letter used for it is irrelevant—and may, in fact, be re-used elsewhere to define an entirely different and independent region. In other words, do not tie letters to regions in any way, other than using them during the region-extraction process itself.

Part 2

This is largely the same as Part 1; just replace the perimeter function with a side-count function.

Identify...

...all the top-side, left-side, right-side, and bottom-side edges (i.e., fence segments), respectively, for each plot within the region.

For each of these categories...

...sort by either row or column grid-coordinate—column for vertical edges, row for horizontal edges—then itertools.groupby the results, and then sort each of those subgroups by the other grid-coordinate. You'll need to identify any discontinuities that result.

An interesting alternative approach is...

...to count all the corners instead of edges. The two numbers are necessarily equivalent, and it may be simpler to identify corners than doing all the edge bookkeeping with sorting and discontinuity identification, etc.

** Day 13: Claw Contraption – Maximizing claw-machine prize count while minimizing costs

Part 1

In retrospect, my approach for solving this one is almost embarrassing. Ultimately, it worked fine, but there's a vastly superior approach. I used dynamic programming for this part and basically brute-forced it through recursion. But, there's a much better and more direct way. Just think carefully about what the problem is actually describing...

Part 2

This is where you must determine a better way, and what I noticed here—after staring at it with my mind blank for a while—made my Part 1 approach look pretty bad by comparison because this method is blazing fast since it's so direct.

The key insight is...

...a combination of two things:

Each button press is...

...a step in a constant direction (for A and B, respectively, independently), i.e., a step along a never-changing line-slope for each button.

Addition...

...is commutative. So, only the step counts in the "Button A direction" and "Button B direction", respectively, matter. This means that, effectively, every press of Button A steps along the same line, and likewise for Button B. The order in which you take those steps is irrelevant; you end up with the same result for the same step counts. For a visualization of this, see the example diagram below, which shows a sampling of possible paths from the starting point (bottom left) to the target destination (top right) by taking 5 steps in one direction and 4 steps in the other. The order in which you take those steps does not matter; all the paths yield the same result, and they all lie within the shown "outer envelope" between the gray and white paths; none can stray outside that and still make it to the target. Therefore, we may pick any of these paths as a convenient representation for our purposes in solving the problem, and I suggest either the gray or the white path because then the problem effectively reduces to just solving for a line intersecting with a line.

And also...

...checking if that intersection falls exactly on integer coordinates (i.e., whole steps, since fractional steps aren't allowed).

The math...

Let the movement for Button A be $\vec{A} = [A_{x}, A_{y}]$ , movement for Button B be $\vec{B} = [B_{x}, B_{y}]$ , the target destination be $T = [T_{x}, T_{y}]$ (and starting point be $S = [0, 0]$ , i.e., the origin), and the number of steps we take in directions $\vec{A}$ and $\vec{B}$ , respectively, be $a$ and $b$ . Then, we need to solve the equation $S + a \vec{A} + b \vec{B} = T$ , which means solving for $a$ and $b$ in these equations:
$a A_{x} + b B_{x} = T_{x}$ and
$a A_{y} + b B_{y} = T_{y}$ .

Multiplying the first equation by $B_{y}$ , and the second by $B_{x}$ , then subtracting one from the other, we get:
$a B_{y} A_{x} + b B_{y} B_{x} = B_{y} T_{x}$ and
$a B_{x} A_{y} + b B_{x} B_{y} = B_{x} T_{y}$ , yielding
$(a B_{y} A_{x} + b B_{y} B_{x}) - (a B_{x} A_{y} + b B_{x} B_{y}) = B_{y} T_{x} - B_{x} T_{y}$
$⟹ a = \frac{B_{y} T_{x} - B_{x} T_{y}}{B_{y} A_{x} - B_{x} A_{y}}$ .

Plug that back into an earlier equation to compute $b$ :
$a A_{x} + b B_{x} = T_{x}$
$⟹ b = \frac{T_{x} - a A_{x}}{B_{x}}$ .

Don't forget you still need to [dis]confirm...

...integer values for these step counts. If either $a$ or $b$ is non-integral, then there is no solution to the problem.

I'd suggest doing this by...

...using integer-division for computing both $a$ and $b$ , then plugging those values back into the original equation to see if it still holds true. If either part does not, then fail. In other words, when using integer division, both of these must evaluate to True for it to be an actual solution:
$a A_{x} + b B_{x} \overset{?}{=} T_{x}$ and $a A_{y} + b B_{y} \overset{?}{=} T_{y}$ .

** Day 14: Restroom Redoubt – Robots moving in wrap-around lines on a grid, and a Christmas tree shape

Part 1

This is pretty straightforward to solve in the obvious/naïve way, iterating through one "second" at a time until you get to the "frame" for the 100th second, then compute the safety factor at that point.

Hopefully, it's obvious to use...

...the modulus operator a lot.

It's probably worthwhile noting that...

...you don't actually need to iterate one second at a time but rather can direct-compute to the 100th-second frame by multiplying by 100 in the velocity addition, then doing the modulus operations.

Part 2

I have mixed feelings about this one due to its vagueness of objective. (Initially, I reacted fairly negatively to it, but I've since come around to feeling a bit more positively toward it.) The target result is so incredibly under-defined in terms of its actual details that you don't really have anything concrete to even look for, algorithmically speaking. Is it an outline shape? A solid (filled-in) shape? A simple triangle (e.g., like the overall event art for AoC 2015)? Something with more jagged edges? What, specifically, is meant by "most" of the robots aligning themselves? How big/small is the shape? Do they align themselves into the shape in the center of the grid, or can it happen anywhere within it? Etc. ?!

Also, I was initially worried that, having done a lot of AoC problems in the past, what it meant here by "rarely" was one time in, say, trillions.

However, upon considering it more...

...it became clear that the upper limit for a repeat cycle length must be the width (101) times the height (103) of the grid. This is guaranteed a wrap-around modulus of 0 in both directions (no matter what the respective velocities are, because velocity*101*103 absolutely is evenly divisible by both 101 and 103), resulting in all the robots being exactly back at their starting positions on that iteration, where they begin a repeat cycle. It'd be possible to have cycles earlier than that, but not later, but since both 101 and 103 are prime numbers, then the repeat cycle length must also be at least that long. Therefore, the expected repeat-cycle length is 101*103=10,403 iterations, which is a far more manageable frame-set size to check (than trillions), albeit still somewhat annoyingly large, especially for having no good specific target definition to look for. (Side note: I did check this repeat-cycle reasoning against the facts, and it was correct; it started repeating at exactly that iteration.)

I also had a sneaking suspicion...

...that maybe what was done in Part 1 was a subtle nudge in the right direction for Part 2.

It...

...could be used that way. It's possible to apply a technique similar to Part 1's to various parts of the grid each iteration, looking for robot counts above some threshold, and thereby auto-identify at which second (iteration) the alignment happens, but it may take a bit of threshold-tuning to get it right and isn't very satisfying as a broadly applicable solution.

One other thing to note is that...

...in the early-ish frames (<100?), you'll see some frames containing what appears to be partially aligned "static" in either a horizontal or vertical direction. Those are indications of where the tree shape will eventually appear, so—if desired—you can narrow down exactly where to target your robot-count checks each frame (rather than searching the whole grid space every frame). In short, they're indications of the repeat-cycle lengths in the vertical and horizontal directions, respectively.

Addendum: After having already gotten the answer, I created an html file with some JavaScript that generated all the frames in an entire repeat cycle, drawn as little canvases with each robot being a single pixel within each frame's canvas. In order to keep the displayed canvas count more manageable, I generated them on a "paged" basis that could be flipped through, forward and backward, viewing just a count-per-page number of frames at a time. The tree-image frame leaps out quite clearly from that [very long] series of frames.

Addendum 2: After chatting with a friend about this one, and thinking about it some more...

...I realized a much more satisfying solution approach to this is to build a neighbor-count histogram of each frame (including diagonals, or not; either works) for all the robots. If the tree shape were only an outline, the histogram total for "2 neighbors" for that frame should spike unusually high; and, if it were a solid shape, the histogram totals for "8 neighbors" (or 4, if diagonals aren't included as neighbors) should spike.

In fact, it further occurred to me that...

...since I already knew what the actual aligned shape looks like, both the filled-shape and outline-shape histogram spikes should happen on the correct frame, due to the "picture frame" drawn around the tree shape! And, this fact made me suspicious this was intentionally done in order to help trigger both the different search strategies at the right time.

I went back and implemented this very simple technique, and sure enough, all combinations nailed exactly the correct frame: both the 2-neighbor and 4-neighbor histogram counts (for excluding diagonal robots as neighbors) and the 2-neighbor and 8-neighbor counts (for including them) had their maximum histogram values for those specific count-entries occur on the tree-image iteration, across all the frames in the repeat-cycle.

(Friend) Counterpoint: ha ha ha, I actually loved this one. I enjoyed the vagueness of Part 2, knowing there was "something" there and having to come up with a detection mechanism without knowing what I was detecting.

What to detect?

I was pretty sure the end result would be ASCII art, so I started with a draw() function to print robots in the grid. First try – manual inspection of every frame. Got a few hundred frames in and decided I needed some actual detection logic. My strategy was to identify candidate frames based on some criteria, and then draw those for more manual inspection.

Candidate identification strategies

First try was border detection. Look for a frame with robots all along the outside edges. This was a bust, no frames identified.

I considered using entropy, on the theory that entropy would drop considerably on the frame with ASCII art. However, I was too lazy to write a Shannon entropy function, so I decided instead to feed the string data for the frame into zlib and compress it. I then drew only frames whose compressed size was the smallest seen so far. Seemed like a cheap and easy way to simulate entropy calculation. Unfortunately, it didn't find the right frame.

What actually worked

Finally, I decided I needed to calculate a count of neighbors for each robot, assuming that the ASCII art would cluster many robots in the same area. I then determined the total count of neighbors for all robots, and only drew a candidate frame if the total number of neighbors was greater than the highest number seen so far. I let this run, and saw a Christmas tree flash by.

In retrospect, because the tree was drawn with solid blocks of robots, I found I could find this frame without any intervening frames by detecting a robot with exactly 8 neighbors. (I counted the diagonal neighbors in addition to up/down and left/right.) This never occurred in my data until the frame with the ASCII art.

** Day 15: Warehouse Woes – Robots moving deterministically in warehouses containing boxes

Part 1

(Friend) This was mostly straightforward; just implement the rules to move the robot according to the sequence of directions.

Tips

Add a function to draw the grid. Otherwise, it's hard to determine whether your code is actually working.

A dictionary mapping the "<>v^" direction chars to point deltas ( (-1, 0), (1, 0), (0, 1), (0, -1) ) is helpful.

Recursion works well to handle moves that end up pushing boxes. There are three possible cases on a potential move:

Move into a wall ('#'): base case, do nothing
Move into empty space ('.'): base case, swap the thing moving with the place it's trying to move
Move into a box ('O'): recursion case, move the box in the same direction, if it succeeds, swap, if not do nothing

(Me) I did this via iteration rather than recursion, which may have resulted in a bit more code but also meant I only needed to adjust the endpoints of any actual movements, leaving the middle stretches untouched in the bookkeeping. Still not too bad.

Part 2

(Friend) There are lots of ways to handle this one. Each box is now two spaces wide, enabling many more types of movement.

There's probably a better way but...

...(friend) took the approach of treating robot moves and box moves differently, and for box moves, treated horizontal and vertical movement differently. (Me: I also treated horizontal and vertical movements differently.) Robot moves are pretty easy and mostly the same as Part 1, except that if you encounter a box, instead of recursing you call a horizontal or vertical box move depending on the direction of movement.

For boxes, horizontal moves are still essentially the same as in Part 1. There's a little fiddliness to making sure each box moves as a unit, but the movement itself is the same. (Me: Same thing here as in Part 1, except I had to back-iterate through the actual movements on this one since I couldn't only adjust the aggregate-move endpoints alone; i.e., I couldn't just leave the middle stretches untouched.)

Vertical box moves are considerably trickier since the boxes can fan out.

I had a lot of issues trying to adapt my Part 1 approach to vertical box moves, until...

...instead of determining whether a box can move and performing the moving in the same function, I have a separate recursive "canmove" function to check all boxes that would be affected by a move to see if any of them hit a wall. In the process of doing this, I built a set of those boxes (actually the coordinates of their left side). Then, if the entire recursive check succeeds, I can perform the moves on the contents of the set, sorted by vertical position, so the moves are all simple swaps.

(Me) I again used iteration for this one, building a "distance layered" list of boxes outward from the attempted push point until either all boxes were found to be able to move, or a single one of them encountered a wall in its "next layer out", in which case the whole process instantly terminated and moved on to handling the next robot [attempted] move. If they were all determined to be able to move, I again back-iterated through the list, moving each until collapsed all the way back to the robot. I did a bit of fancy "move dictionary" lookup for automatically adding in both parts of the boxes while building the outward-growing layers. I.e., if trying to push "^" (which is a (row,col) delta of (-1, 0)) and encountering a box, that means finding either "[" or "]"; obviously, that gets added to the currently building layer's set of items to move, but it also means needing to add in its other half, which can be directly looked up by movement+boxpiece as a key. That is, the "move dictionary" can contain "move" keys of "^[" and "^]", as well as "v[" and "v]", with corresponding values of (-1, 1), (-1, -1), (1, 1), and (1, -1) as respective deltas for where the other half of the encountered box is located.

** Day 16: Reindeer Maze – Finding the minimum movement score through a maze between start and end points (and the best seats for watching it happen)

Part 1

(Friend) For this style of path-finding problem, I like using a work queue. Initialize the queue with the current state (position, heading, score), and then repeat while the queue isn't empty. Also create a dictionary to track the score for positions-&-headings that have been visited. For each iteration, pop the head of the queue, then determine all next possible states (move forward, turn left, turn right), and append them to the queue if they haven't been visited yet or if the resulting score would be less than the existing score for that position-&-heading. If the position is the end point, update the "best" score seen so far if it is less than any previous best score.

Once the work queue is empty, you've found the best score.

(Me) It sounds like I did something nearly identical for this one, with two minor notes:

I recorded minimal scores found for every position-&-heading for all of the non-wall positions (including the end position), building a dictionary of this information until there remained nothing left to handle. After all this was complete, there were one or more heading-entries associated with the end-position, from which I only then selected the minimal one to return as the result.
I also processed moves slightly differently, with each position-&-heading state being able to do one of the following: one step forward (+1 score), turn left then one step forward (+1000+1 score), or turn right then one step forward (+1000+1 score). This enabled me to always be able to "look ahead" to determine if I even could physically make such a move (i.e., is there a wall there?), and only add it to the work queue if I could. (Note that the only other potential option here is to fully turn around then step forward (+1000+1000+1 score), but thinking about this a bit led me to the conclusion that this will always eventually result in worse scores than other possibilities, so there's no need to include it at all.)

Part 2

(Friend) I used the approach from Part 1, but added an additional component to the state; a set containing all coordinates visited so far. I also keep a global set of all "best path" coordinates. At each step, I update the state's coordinate set for forward moves. (There's no need to change it for turns.) Then, whenever a path is found, if the score is less than the best seen so far, I replace the global set with the set from that state. If the score is equal to the best seen so far, I update the global set with the coordinates from the new states set (i.e., make it be the union of the global set and the new set, but do it in-place via the "update" method).

(Me) I used the min-score dictionary I built in Part 1 to select the set of optimal scores at the end position (one or more), then ran those backward through the min-score dictionary, building a best-paths'-positions dictionary as I went. At each reverse-step, I again explored all the options (a step backward (-1 score), a step backward and a turn right (-1-1000 score), and a step backward and a turn left (-1-1000 score)), but this time I imposed the more stringent constraint that a step is only allowed if (it's not a wall and) its score exactly matches the minimal reversing-score.

** Day 17: Chronospatial Computer – A strange, mostly-3-bit computer with 8 instructions

Part 1

This Part is not too terribly difficult, though it does require exacting attention to detail. Just read the description very carefully, and meticulously implement it, one piece at a time.

Part 2

You'll need to be a bit more clever with this part because, realistically, it's not ever going to finish running if you take the naïve approach of just starting register A's value at 0 and iteratively incrementing it and checking to see if that's the answer. You'll need to use the functionality of the program itself to determine how to generate the value in register A much more directly. So, you'll need to study it more closely in order to figure out what matters and how to leverage it.

You'll want to use...

...int(string, 2) and f"{integer:03b}", and/or perhaps octal.

It may help to "decompose" the program: for example, its core output computation can be written as a single Python expression.

(Friend) I also found it helpful to just run the program and dump diagnostic output to get a sense of what's happening. For example, try running it by iterating over different start values for A – say from 0 to 0x1000. For each iteration, if you match one or more of the expected output values, print the start A value and the number of output values. Try dumping the A value in both octal and binary (e.g., f'{a:o} {a:b}').

But, there are key insights...

(Me) ...for the "reverse" approach...

...where the program is processed in reverse order so that the necessary value to start with in register A gets generated from left to right. Using this strategy, each 3-bit position within A can be examined for only its eight possibilities (0 through 7)—in combination with whatever has been generated on the way to reaching it, of course. (I.e., each gets appended to what's come before, and evaluated.) There's a bit more to it than that because each position may result in zero or more numbers that produce the necessary output (depending on how you reached the position), but that's a massive push in a workable direction.

I used...

...recursion to traverse through all the possibilities using this approach, selecting the minimal result, and it completed essentially instantly.

You'll still need to handle the dead-end/no-options cases...

...such as by returning math.inf for them, so they're never selected as the minimum value.

(Friend) ...for the "forward" approach...

...where the program is processed in forward order so that the necessary value to start with in register A gets generated from right to left. For each value in the expected output, which bits of register A can possibly influence it? Use analysis of the program itself, combined with diagnostic output...

...to determine...

...that there is a 10-bit "window" that can contribute to each output. The window shifts by three bits for each output:

      Register A
   2         1         0
...098765432109876543210
     |  |  |  |--|--|--+ output 0: bits 0-9
     |  |  +--|--|--+ output 1: bits 3-12
     |  +-----|--+ output 2: bits 6-15
     +--------+ output 3: bits 9-18
             ...

Use this 10-bit window...

...to iterate over all possible 10-bit values (there are only $2^{10} = 1024$ in total) for register A, run the program, and if it produces the expected output, add it to a list of candidate values.

Now that you have the initial set of candidates, you can prepend 3 bits at a time to generate a new list of candidates for each additional output value.

for each candidate starting register A value:
xxxxxxxxxx --+-> 000xxxxxxxxxx
             +-> 001xxxxxxxxxx
             +-> 010xxxxxxxxxx
             +-> 011xxxxxxxxxx
             +-> 100xxxxxxxxxx
             +-> 101xxxxxxxxxx
             +-> 110xxxxxxxxxx
             +-> 111xxxxxxxxxx

For every new candidate, run the program; if you match the next output value, keep the new candidate, otherwise discard it. Repeat until you have all starting values for A that yield the necessary output. You'll have multiple possibilities. Select the smallest one.

Note that you don't have to run the full program each time. You can just run a single iteration for each candidate value on the current 10-bit window.

** Day 18: RAM Run – Traversing a grid from upper left to lower right while avoiding invalid locations

Part 1

I was surprised to see this problem following some of the others already seen.

It's a straightforward...

...Breadth First Search problem, and I thought it was substantially simpler to solve than were several earlier problems.

Part 2

This Part was also quite straightforward, though not necessarily in any sort of notably efficient way. For example, it could just be done by iterating in single steps through adding the byte-drops that are corrupting memory, and checking for being able to reach from upper-left to lower-right on each round. Until you can't. And, the first time it's impossible means the location of the most recently dropped byte is the answer requested. (A very obvious optimization for this approach is to start the process at 1024 bytes dropped since, from Part 1, you already know the path is not yet blocked at that point.)

Even using this simple approach, you can do substantially better...

...such as by using a binary-search strategy to far more quickly converge on when the path-block occurs. I.e., check if it's blocked at a point where the number of bytes dropped is halfway between 1024 and the total number of droppable bytes; if yes, check the halfway point between that point and 1024; if no, check the halfway point between that point and the total droppable byte count. Continue halving the remaining pool of possibilities until there's convergence on the first point where the path becomes blocked. This finds the answer far faster.

There are even more efficient ways...

...with one such way being to treat the corrupted byte locations as a sort of stepping stone to see if you can traverse from the left/bottom edges to the top/right edges by only moving to their neighbors (with diagonals included). If this is possible, then it means the (non-corrupted) pathway from upper left to lower right is blocked (since it only moves horizontally/vertically, not diagonally). This requires far less time to determine (perhaps via BFS again) because not only are there fewer corrupted blocks to check, but also, almost by definition, many/most of them aren't connected to each other at all, so they're never even reached/checked by the BFS, meaning it converges to a result even faster.

Also, this approach can be combined with the binary-search strategy already described above to speed things up even more.

And, it's quite possible there are yet better ways than these... ? But, these already make it pretty fast.

** Day 19: Linen Layout – Striped towels used to (try to) create desired patterns

Part 1

I was even more surprised this problem was yet easier than Day 18's, which was already surprisingly easier than earlier problems.

This problem's solution was quite straightforward if leveraging...

...dynamic programming.

I did make one optimization...

...where I built a towel dictionary containing sets of towels keyed to their respective first letters, which substantially reduced the number of towels to iterate through when checking for those that have even a chance of matching segments in the desired pattern.

Part 2

Slightly tweak Part 1's solution.

** Day 20: Race Condition – Racing with one allowed cheat

Part 1

This seemed like basically a simplified variation on Day 16's Part 1, plus a bit of work after that set-up. I thought it was yet again easier than some earlier problems, except...

...don't forget to...

...account for the "cheat time" itself! I.e., the 2 picoseconds required to traverse the cheat distance. I very stupidly forgot to include this in my inequality check, and it resulted in me taking roughly twice as long to solve the overall problem (both Parts) than it otherwise would have, due to having a hard time tracking down that single issue in my code! Oof!

Part 2

This is substantially the same as Part 1, but extended more.

A helpful observation...

...is that the cheat area to check is neatly bounded by the Manhattan Distance diamonds determined by the sum of the magnitudes of the delta-row and delta-column (relative to the potential cheat's start-point) being lower-bounded by 2 and upper-bounded by 20: $2 \leq | 𝐝 r | + | 𝐝 c | \leq 20$ . This is relatively straightforward to just loop through directly. Note that the (minimal) "cheat time" is also just this sum, for any location being evaluated within this hollowed-out diamond.

Visually, the inequality relationship looks like this.

                                        x   <-------- 20 steps away from center o
                                      x x x                                     |
                                    x x x x x                                   |
                                  x x x x x x x                                 |
                                x x x x x x x x x                               |
                              x x x x x x x x x x x                             |
                            x x x x x x x x x x x x x                           |
                          x x x x x x x x x x x x x x x                         |
                        x x x x x x x x x x x x x x x x x                       |
                      x x x x x x x x x x x x x x x x x x x                     |
                    x x x x x x x x x x x x x x x x x x x x x                   |
                  x x x x x x x x x x x x x x x x x x x x x x x                 |
                x x x x x x x x x x x x x x x x x x x x x x x x x               |
              x x x x x x x x x x x x x x x x x x x x x x x x x x x             |
            x x x x x x x x x x x x x x x x x x x x x x x x x x x x x           |
          x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x         |
        x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x       |
      x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x     |
    x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x   v
  x x x x x x x x x x x x x x x x x x x   x x x x x x x x x x x x x x x x x x x
x x x x x x x x x x x x x x x x x x x   o   x x x x x x x x x x x x x x x x x x x
  x x x x x x x x x x x x x x x x x x x   x x x x x x x x x x x x x x x x x x x
    x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
      x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
        x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
          x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
            x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
              x x x x x x x x x x x x x x x x x x x x x x x x x x x
                x x x x x x x x x x x x x x x x x x x x x x x x x
                  x x x x x x x x x x x x x x x x x x x x x x x
                    x x x x x x x x x x x x x x x x x x x x x
                      x x x x x x x x x x x x x x x x x x x
                        x x x x x x x x x x x x x x x x x
                          x x x x x x x x x x x x x x x
                            x x x x x x x x x x x x x
                              x x x x x x x x x x x
                                x x x x x x x x x
                                  x x x x x x x
                                    x x x x x
                                      x x x
                                        x

** Day 21: Keypad Conundrum – Direction-pad used to control a robot, to control a robot, ..., to control a robot to type a numpad code

Part 1

This can be solved in a variety of ways since there's no significant computational constraint.

It did intuitively seem clear to me that...

...even though there are potentially quite a few possible ways to directionally get from one button to another (e.g., if they're far apart from each other on the numpad) that the best routes must necessarily be either all-horizontal-then-all-vertical or all-vertical-then-all-horizontal. This is because any additional swapping back and forth between horizontal and vertical directions would increasingly lengthen direction expansions with successive direction-pad levels. Though it's not strictly necessary, I did apply this intuition to my code (in both Parts), and it yielded the correct results. This strategy prunes the paths to explore from potentially quite a few down to just one or, at most, two for each button-to-button transition. (Note that using this approach, even quite a few of the would-be two-path options are cut down to only one because of the non-rectangular shape of the pads, i.e., a fair number of would-be-two paths fall off the pad for one path but not the other, in which case there's only one valid path.)

Of course, this is irrelevant at the "outermost" level of direction-pad since that sequence is not further expanded. So, any sort of flipping back and forth between horizontal and vertical directions would be fine there. (Though, no matter what direction combination is used there, the length results are the same since, e.g., these are all length three: ^^>, ^>^, >^^.)

Part 2

This one has much greater computational constraints, and it took me way too long to get my head wrapped around it, but eventually I landed on what I'm sure was the expected solution. Even early on, I was pretty sure I knew the right solution strategy to use, but it took me substantially more time than it should have to figure out how to use it since I'd solved Part 1 a bit differently. (As usual, in retrospect, it should have been fairly obvious. But, it just wasn't, for me, for a long time.)

The way I solved it was...

...to formulate the solution code in a way conducive to using dynamic programming.

You just need to...

...recursively express how to expand each direction-pad sequence to the next level of direction-pad. (This may all be done after pre-expanding everything at the numpad level, so all the recursive code is exclusively dealing with direction-pad details. Pre-expanding like this may yield several possible sequences to explore; simply evaluate them all, and select the shortest.)

For each sequence level...

...expand each individual character into the necessary direction-pad button sequence(s) to produce it, and recurse until you're at the necessary level, at which point you return the length. If you're not yet at the target level, sum each recursion sequence option and select the minimum length among them, returning that back to the previous level.

Observe that, in order for this to work, it is vitally important that...

...every character expansion into a direction-pad sequence begins and ends on the 'A' key (in order to produce the button press at the previous level). Were this not the case, this strategy would not work because recursive calls would not be independent of sequentially-earlier button presses. (Though, perhaps it would be possible to also handle that situation somehow.)

** Day 22: Monkey Market – A monkey market, secret numbers, and predicting results from length-four sequences

Part 1

Just pay close attention to what the description says, and carefully implement the details.

Part 2

Probably the most challenging component to solving this problem is just trying to figure out how to definitively identify all length-four sequences across all monkeys. Fundamentally, that's the only new element introduced in Part 2.

I wrestled for a short time with how to do this, until I realized I could...

...actually process every monkey series exactly one time, ever.

Instead of trying to cleverly generate and cycle through all the potential length-four sequences...

...I turned the whole process on its head and just used every length-four sequence actually present in each of the monkey series.

Once I hit upon this approach, I simply...

...accumulated each of their length-four-first-appearance values (in each monkey series) in a dictionary keyed to them as 4-tuples, then selected the max value from the dictionary contents at the end.

** Day 23: LAN Party – Identifying three-way-connected computers in a network (and maximum cliques in a graph)

Part 1

This Part isn't bad if you've built the connectivity representation nicely since it only requires identifying all computer pairs within a given computer's connections that are also connected to each other (and making sure to count each triple only once, of course—and only those containing at least one computer with a 't' name).

Part 2

This is the problem of identifying a maximum clique within a graph, which is an NP-complete problem.

For the given scales of data...

...this can easily be brute-forced by cycling through all combinations of each subset size (from largest down to smallest) for each computer's connections, while—importantly!—tracking largest-clique-found-so-far and pruning all checks that can't possibly yield larger results.

** Day 24: Crossed Wires – Simulating a system of XOR, AND, and OR logic gates wired together

Part 1

Just carefully implement the details of what the description says. It'll probably include some dictionaries, and perhaps frozensets.

Part 2

I don't have a purely algorithmic approach to recommend here since I basically just used code as an incremental forensic tool to interactively assess the circuitry.

Specifically, I...

...noted that the problem says gate outputs got swapped, not gate inputs. This is important because it means all gate input connections are correct; only the output connections may be incorrect.

A correctly constructed adder circuit—see below—should have only XOR gates outputting to the z## output wires, except for the most significant bit, which should be an OR gate's output. So, I back-traced all the z## output(?) wires to their respective gates, i.e., those outputting to them. This back-trace identified three incorrectly connected wires (connected to the wrong type of logic gate) for my given problem input data.

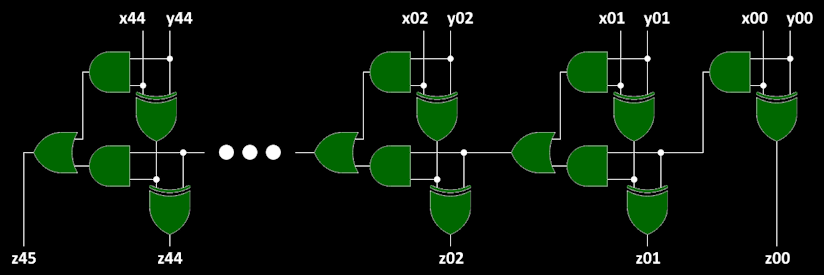
I also...

...took advantage of the fact that, since all the gates' inputs are correct, then all of the circuit's x## and y## input wires are definitely correctly connected to their respective XOR and AND gates. This meant I could identify exactly which XOR gates must be connected to output wires, i.e., z## wires—any of them, whether or not they're the correct ones. That is, all those XOR gates not connected to circuit inputs x## and y## wires are supposed to be connected to z## wires for output (except for the least significant bit, which should be connected to all three). From this subset of XOR gates, I identified all those not connected to z## wires, which produced another three results for my problem input data, and I was able to pair these with the previous erroneous-gate-output results to determine three of the four wire swaps.

I then had one more problematic gate-output-pair to identify...

...I corrected the three erroneously swapped output pairs then repeatedly simulated the resulting circuit with carefully selected input test vectors, comparing the results to known-correct results.

Specifically, I ran through inputs of...

...all-zero y## with x## values iterating through a single 1-bit shifted incrementally leftward, which should yield z=x as output, in each case. These inputs exercise the "sum paths" through the circuit.

I also iterated through a single 1-bit shifted incrementally leftward for both x## and y## inputs (x=y), which should yield z=2x=2y (either x or y shifted left once more) as output. These inputs exercise the "carry paths" through the circuit.

Examining those circuit-outputs not matching the known-correct results suggested the gate-outputs for a specific XOR and AND gate should be swapped. I did this wire swap, then re-ran the simulations, and they all passed.

From all these identified problem-wire-pairs, I generated the alphabetized answer.

** Day 25: Code Chronicle – Identifying matching locks and keys

Part 1

This problem was also significantly easier than earlier ones.

But, it seemed especially easy if...

...leveraging a simple "matrix transpose": zip(*lock_or_key)

This lets you more directly use Python mechanisms rather than manually coding things up—that is, something like a row_list.count('#') kind of thing.

Part 2

This Part gives you a star for free, providing that final required piece to finish . . . in conjunction with completing all 49 of the preceding Parts of this year's problems.

Advent of Code (AoC) 2024